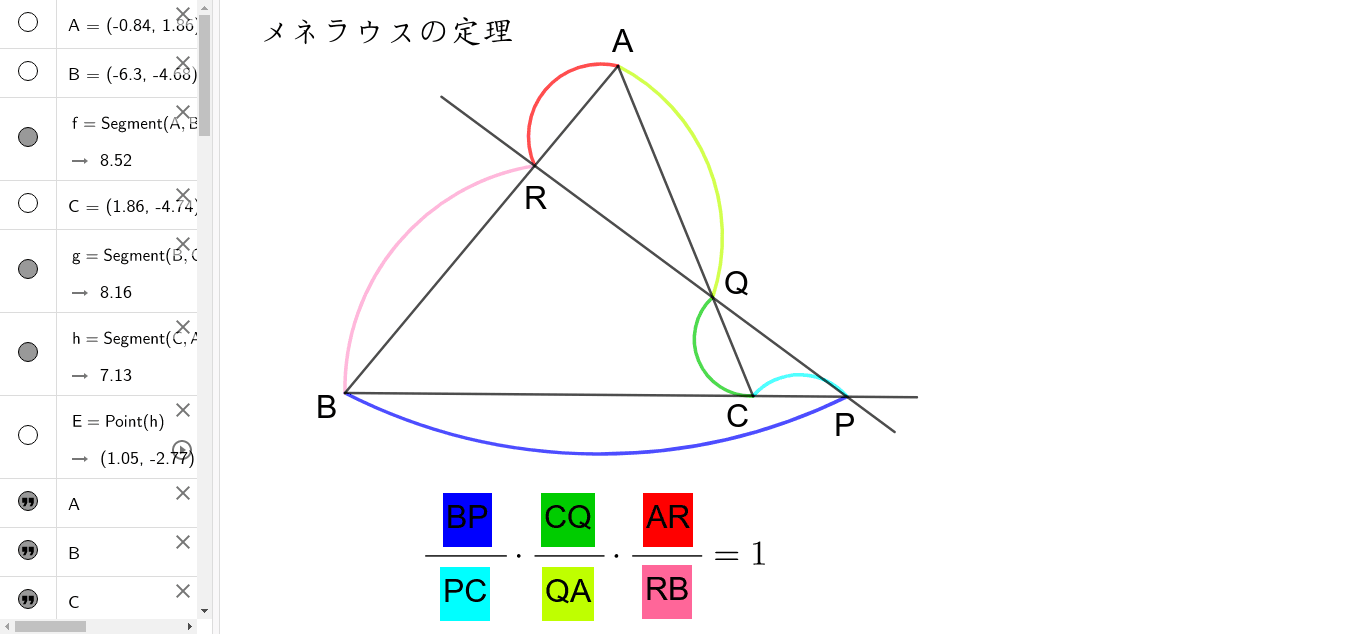
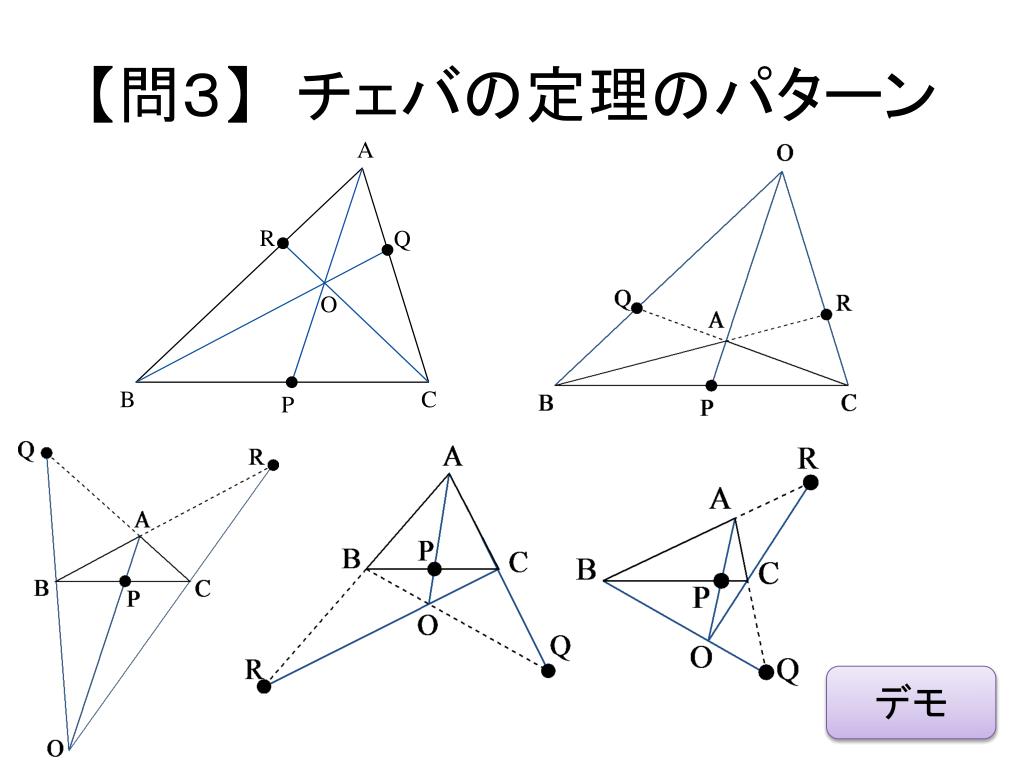
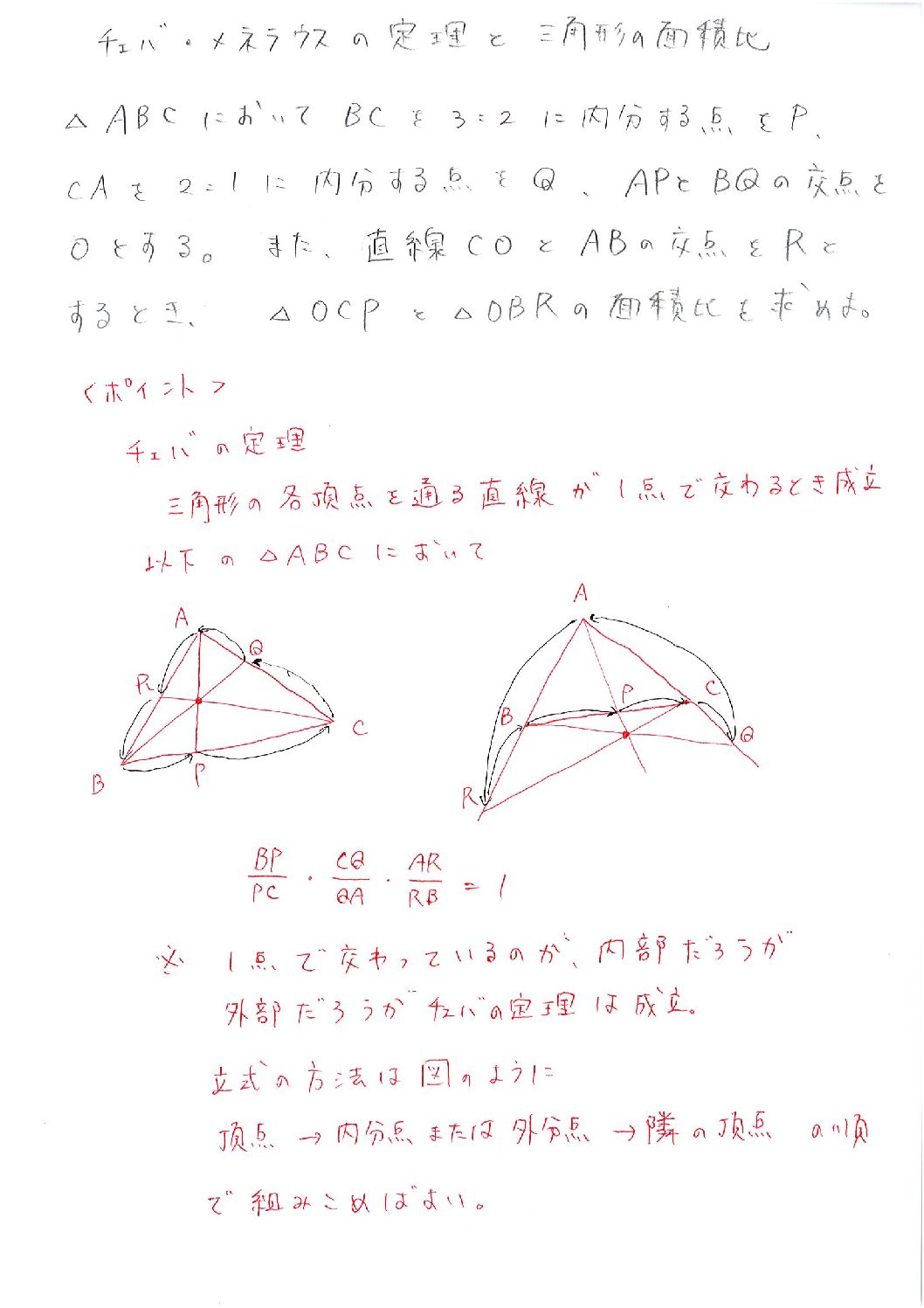
Oct 02, 19チェバ・メネラウスの定理が使えるようになると何が出来るのか メネラウスの定理が使えると、ベクトルの問題で重宝します。 特にセンタータイプの答えだけ入れていくような問題の場合は、大幅に時間を短縮できます。 直接、答えを求める問題でなくメネラウスの定理 チェバの定理 ・性質を形式的に暗記するだけでなく,いろいろな証明法やその考え方を問題解決に結び付けるように指導する。 知識・理解 角の二等分線の性質や与えられた定理を正しく理解できる。 展 開チェバの定理 定理 ABC A B C の頂点 A,B,C A, B, C と, この三角形の辺及びその延長上に無い点 O O を結ぶ 各直線が対辺またはその延長とそれぞれ点 P P, Q Q, R R で交わるとき, 次の等式が成り立つ BP PC ⋅ CQ QA ⋅ AR RB = 1 B P P C ⋅ C Q Q A ⋅ A R R B = 1 この定理では点 O O が三角形の内部にある場合 (左の図)と外側にある場合 (右の図)があります よく使うのは左の図の場合です

高校数学a チェバの定理2 応用 練習編 映像授業のtry It トライイット
チェバの定理 問題 応用
チェバの定理 問題 応用-チェバの定理 (チェバはイタリアの数学者17世紀) abc の辺上にない1点 o をとり, o と頂点 a, b, c を結ぶ直線がそれぞれ辺 ab, bc, ca またはその延長と交わる点を p, q, r とするとき,次の式が成り整数の性質 約数と倍数, ユーグリッドの互除法と1次不定方程式, 分数と小数, n進法




メネラウスの定理 Menelaus S Theorem Japaneseclass Jp
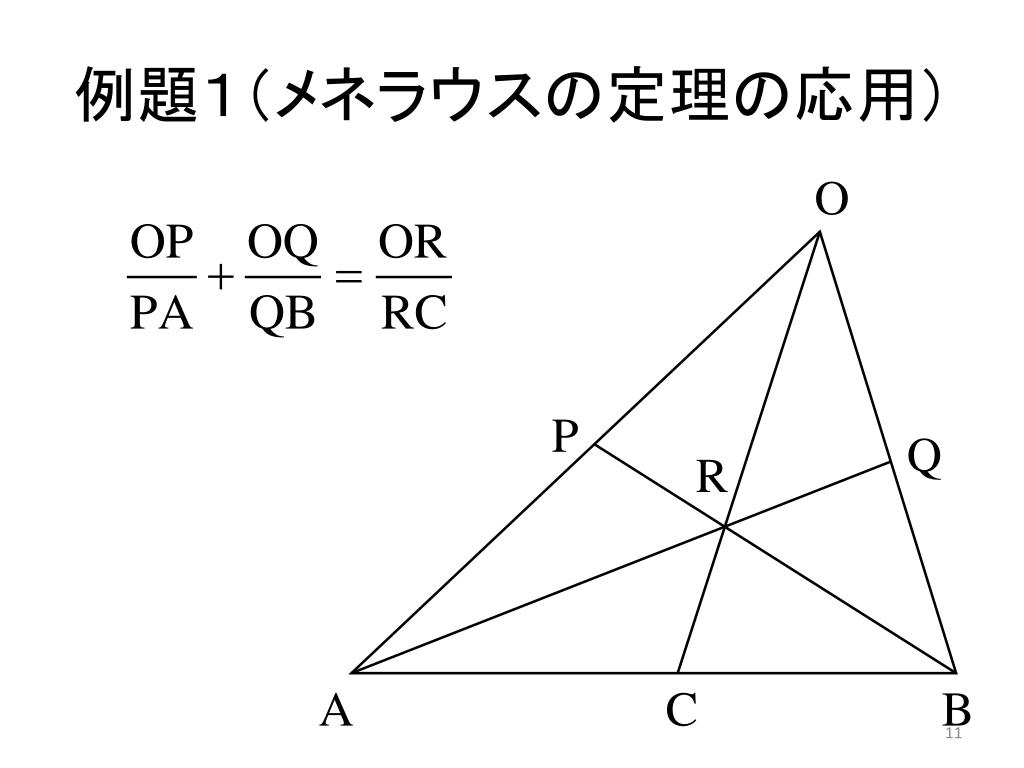
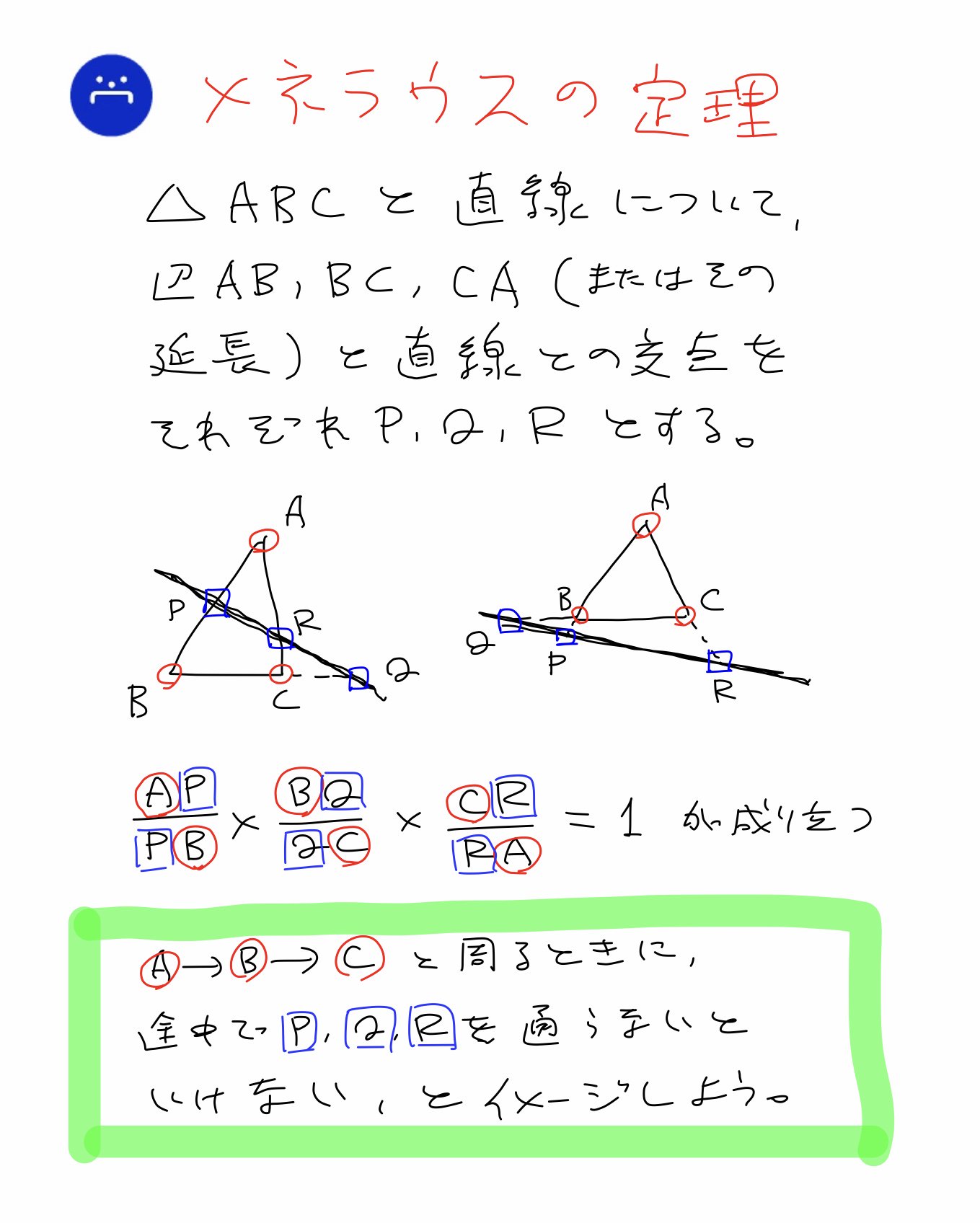
Aug 14, 12abcの辺abを3:2に内分する点をd、辺acを4:3に内分する点をeとし、beとcdの交点をoとする。aoとbc、deの交点をそれぞれf、gとするとき、比 (1)bf:fc (2)dgge をもとめよ。という問題。(1)はそのままチェバの定理の公1 メネラウスの定理 abc の3 辺bc,ca,ab 上,またはそれらの 延長上にそれぞれ三角形の頂点と異なる点p,q,r がある。3 点p,q,r が一直線上にあるならば,次 の等式が成り立つ。 1 rb ar qa cq pc bp ・ ・ = 2 チェバの定理 abc の3 辺bc,ca,ab 上にそれぞれ点p,qこれを, チェバの定理 といいます。 以下のように証明できます。 を通る の平行線と, , の交点をそれぞれ , とすれば, また, , 平面図形 三角形の性質 三角形の辺と角の大小 例題 練習問題 三角形の3辺の大小関係 例題 練習問題
メネ ラウスの定理 チェバの定理 応用公式9 いずれの図でも、ア/イ×ウ/エ×オ/カ=1 です。(/は分数の意味です) (問い) 次の図のような、三角形abcでad,be,cf が点gを通っています。またbdとdcの長さの比は 2:1、aeとecの長さの比は、2:3です。チェバの定理の応用例 ABC の内接円が辺 BC 、CA 、AB と 接する点をそれぞれ P 、Q 、R とする。 このとき、3直線 AP 、BQ 、CR は、1点 で交わる。 (証明) 円外の1点から引いた接線の長さは等しチェバの定理の逆チェバの定理の逆は以下のようなものでしたの辺, , またはその延長上にそれぞれ点, , があり, この3点のうち1個または3個が辺上の点であるとする このとき,とが交わり, かつが成り立つならば, 3直線, , は1点で交わる 今回は, この定理の利用例として, 三角形の重心, 内心
チェバの定理点がひとつあり、各頂点からその点を通る直線が3本ある メネラウスの定理三角形に対して直線が一本ある だと思います ぐみ 4年以上前 ありがとうございます! この回答にコメントする この質問に回答するチェバの定理で点Oが ABCの外にあるときというのは図のような場合ですが,このときも, P:直線AOと直線BCの交点 Q:直線BOと直線ACの交点 R:直線COと直線ABの交点 とすれば,点Oが内部にあるときと同じ という関係式が成り立ちます。 点P, Q ,R の位置をしっかりとつかめば,点Oが ABCの内部か外部かに関係なく という順番,すなわち,頂点→分点→頂点→分点Mar 17, 16チェバの定理の逆 チェバの定理の逆は以下のようなものでした ABC A B C の辺 BC B C, CA C A, AB A B またはその延長上にそれぞれ点 P P, Q Q, R R があり, この3点のうち1個または3個が辺上の点であるとする このとき, BQ B Q と CR C R が交わり, かつ BP PC ⋅ CQ QA ⋅ AR RB = 1 B P P C ⋅ C Q Q A ⋅ A R R B = 1 が成り立つならば, 3直線 AP A P, BQ B Q, CR C R は1点で交わる 今回は, この定理




2 164 Abc P Zbpc Zcpa Apb See How To Solve It At Qanda



メネラウス の 定理 メネラウスの定理
メネラウスの定理の覚え方1 ・メネラウスの定理は「六点からなる(キツネのような形の)図形に対して成立する定理」と認識する立場です。 あとは,順々に比をとっていきます。 比の順番の覚え方は自由です。 ちなみに僕はキツネの頭からはじめて「小,小,大,バック,小,小」と覚えました。 ・分子/分母 = 1 =1 = 1 という主張なので,分母と分子をヒックメネラウスの定理では3点 P, Q, R は1直線上に並びますが,チェバの定理では,それぞれ辺 AB, BC, CA にあります. (公式の見方) 右図のように,頂点 A からスタートして,交点 P までの長さを分子(上)とし,次に,交点 P から頂点 B までの長さを分母(下参考 チェバの定理の証明 右の図で,3 直線 ap ,bq,cr が1 点 o で交わるとき, 線分比と面積比の関係より, bp pc ×



数学i Aチェック リピート 第4章 2図形への応用 9 空間図形への応用 Pukiwiki




慶應生紹介 メネラウスの定理の覚え方はコレだ 証明 問題付き 高校生向け受験応援メディア 受験のミカタ
Keywords:多様な解法、チェバの定理、特殊と一般の関係 1.はじめに 現在多くの児童生徒が「与えられた解法を覚え、 それに数値等を当てはめて問題を解くのが数学の 学習である」という数学に対する閉塞的な学習観 に囚われているという実態がある。1)Sep 16, 18こんにちは。 da Vinch (@mathsouko_vinch)です。 チェバの定理・メネラウスの定理とはまず。チェバの定理とメネラウスの定理は「比に関する定理」です。さらに「三角形に対して使っていく定理」なのでそれを忘れないようにし5方べきの定理を導き、この定理を活用できるようにする 1三角形の辺の比 2時間(本時はその第8時) 2三角形の外心・内心・重心 2時間 3チェバの定理、メネラウスの定理 1時間 4円に内接する四角形 1時間 5円と直線 1時間 6方べきの定理 2時間




高校数学a チェバの定理2 応用 練習編 映像授業のtry It トライイット



メネラウスの定理とは 証明や覚え方 問題の解き方 受験辞典
Jul 15, 18目次 1 数学「チェバの定理」とは? 定理の覚え方や問題(例題)、証明、面積比との関係などをまとめました。 チェバの定理の逆もどうぞ平面図形 中学数学 高校数学 11 チェバの定理が使える図形とは 12 チェバの定理とは? 13 チェバの定理の覚え方 14 チェバの定理を使う問題(例題) 15 チェバの定理と面積比要は,メネラウスの定理やチェバの定理と関係していて,下の図の \(\mbox{AE}\mbox{EB}\) や \(\mbox{OP}\mbox{PE}\) などの比の値が簡単に求められるって話しなんだ。 これって,二つの定理で解けるでしょ。やってみよう。まずはチェバの定理だね中点連結定理の練習問題 練習問題①「辺の長さを求める」 練習問題②「台形の中点を結ぶ」 練習問題③「平行四辺形であることを証明する」




チェバの定理 メネラウスの定理が分からないのは 個人指導シグマ 中高一貫 国立生専門塾



Ppt 数学のかた ち Powerpoint Presentation Free Download Id
May 15, チェバの定理の基本形的な考え方は「ぐるりと一周する」ことです。 よく出題されるのは、交点 o が三角形の内部にある形。まずはこの形を見つけられるようになること、この形で使えるようになることです。 応用として、交点 o が三角形の外部にある形 が登場します。入試問題としては知っておきたいレベル、定期考査なら満点阻止問題レベルとして捉えておきチェバの定理・証明問題 チェバの定理の逆・証明問題 その2 メネラウスの定理・証明問題 メネラウスの定理の逆・証明問題 その2 トレミーの定理 応用問題 角の二等分線の長さ 整数解問題 数学Ⅱ・B 係数分離法から組立除法へMar 11, 21中線定理の3通りの証明 チェバの定理の3通りの証明 スチュワートの定理の証明とその仲間 九点円の定理の証明と諸性質 シュタイナーレームスの定理 根軸の性質と根心の存在定理 三角形の決定条件と自由度 接する2つの円の相似の中心




高校数学a メネラウスの定理2 応用 例題編 映像授業のtry It トライイット
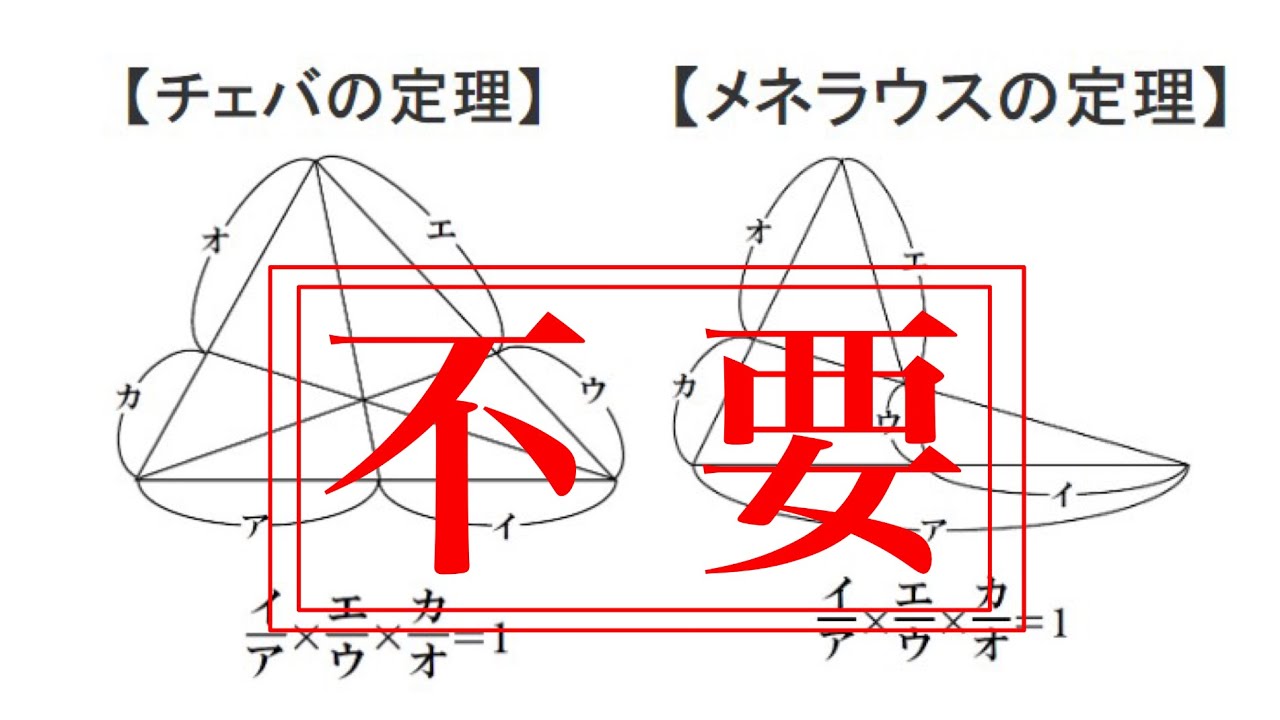



チェバの定理やメネラウスの定理は不要 辺比と面積比の関係だけでカンタンに解く方法を伝授 Youtube
Ar rb = aob coa ×Jul 15, 18数学おじさん今回は、チェバの定理を使える図形を、チェバの定理を使わずに、解いてみようかと思うんじゃ具体的には、以下の問題じゃ数学おじさん上の図で、af bf = 3 2ae c平面図形 九点円の定理 角の二等分線の性質と二等分線の長さ パップスの六角形定理 三角形の合同条件 方べきの定理の証明と例題 チェバの定理とその逆 トレミーの定理とは 多角形の内角



3分で分かる チェバの定理をわかりやすく 証明も徹底解説 合格サプリ
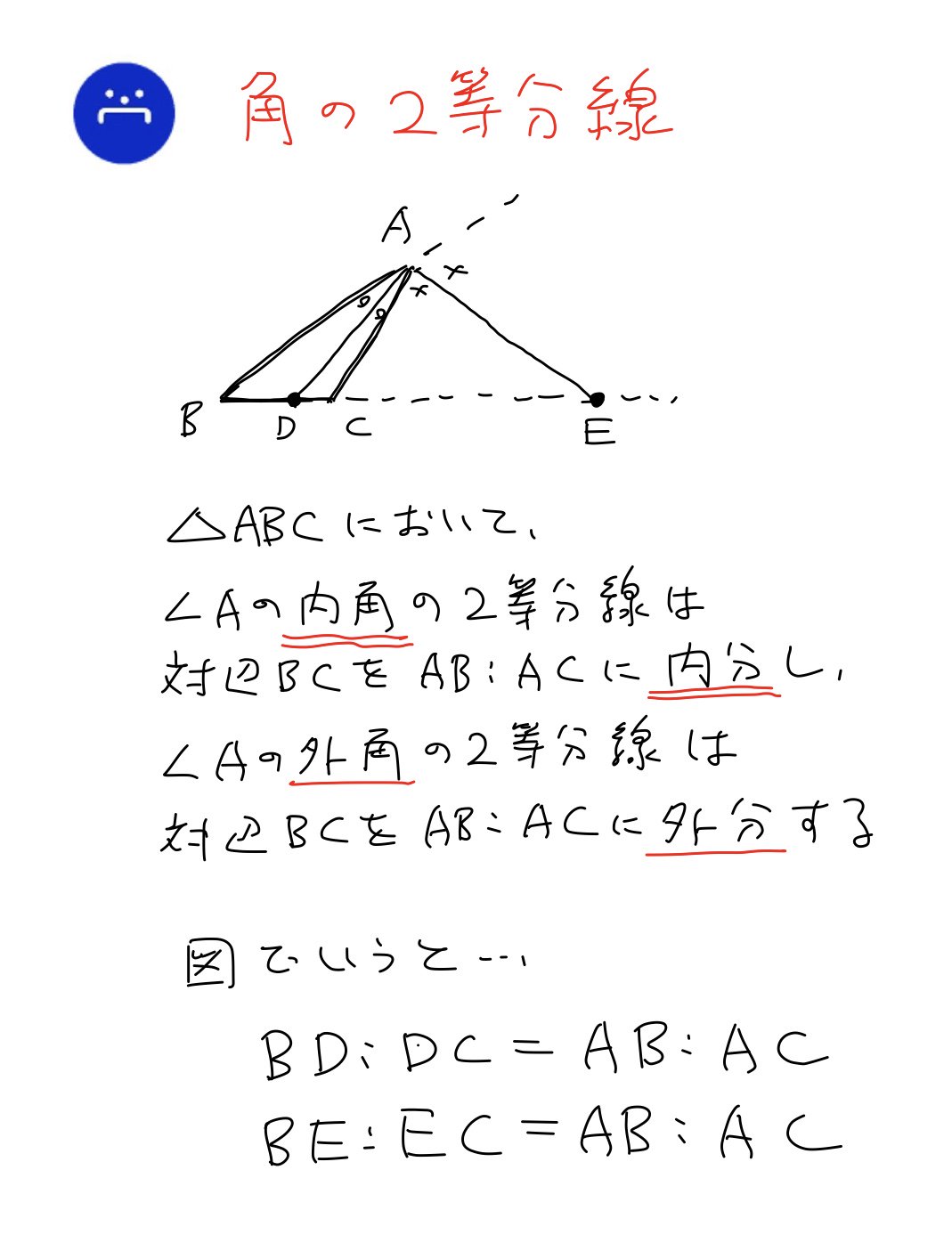



内分 Recherche Sur Twitter Twitter
また, チェバ(1647~1734) はイタリアの数学 者である。チェバの定理は1678 年に発表され た。2 つの定理は一見して似たような定理だが, 2 人の生存していた時期は1500~1600 年も違 う。これは, 何かしら不思議に感じる。 この2 つの定理は連携して色んな応用が平行線と三角形, 三角形と線分の比, 三角形の外心・内心・重心, 円周角, 接弦定理と方べきの定理, 2つの円, チェバ・メネラウスの定理, 作図, 直線と平面, 多面体;May 15, 21今回はメネラウスの定理とチェバの定理について学習しましょう。旧課程のセンター試験ではほとんど出題されませんでしたが、新課程ではよく出題される問題の1つになりました。 近年では、17年のセンター試




箱ひげ図 チェバの定理とメネラウスの定理 あなたは解けますか 1冊でしっかりわかる と大人気のベストセラーシリーズに 待望の高校数学が登場 かんき出版のプレスリリース




高校数学a 方べきの定理3パターンの証明と三角形の相似 受験の月
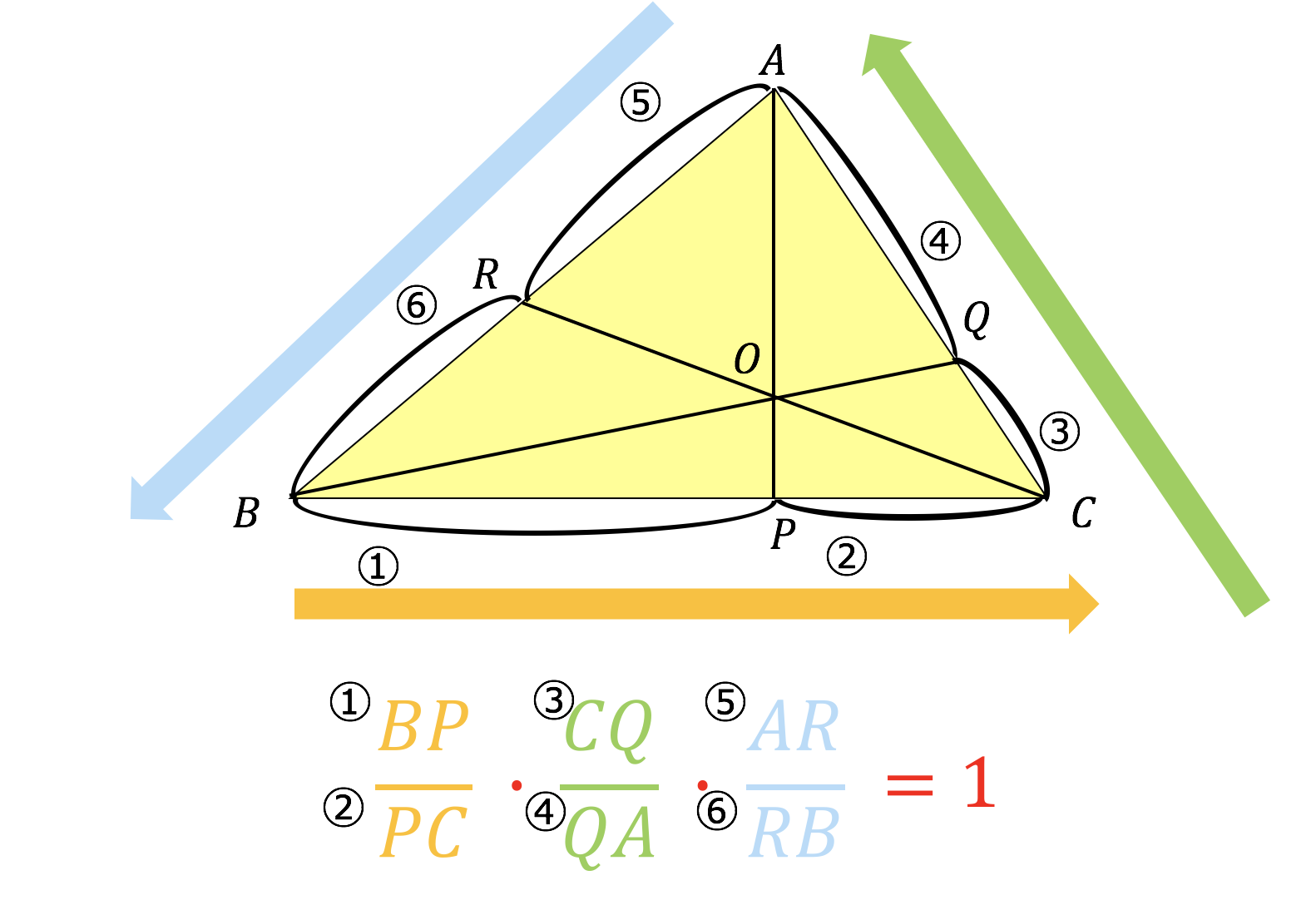
Mar 28, チェバの定理は、三角形の外周を 点を辿りながら順番に \(\bf{1}\) 周するイメージ です。 なお、チェバの定理は辺の比について成り立つので、外周を順番に回ることさえ守れていれば、 項の順序が入れ替わっても問題ありません 。 メネラウスの定理との違い チェバの定理と間違いやすメネラウスの定理・チェバの定理・徹底解剖! センター試験において必須の定理、「メネラウスの定理」です。 「チェバの定理」も類似の定理としてセットで学習しましょう。 チェバの定理 まずは簡単な方、「チェバの定理」です。 こ§33 「チェバの定理」を使う基本例題:その2 §34 「チェバの定理」を使わずに解く §35 「基本例題b~c」の応用例 §4 「メネラウスの定理の逆」と「チェバの定理の逆」 §41 「メネラウスの定理」と「チェバの定理」の言い換え §42 メネラウスの定理の逆




慶應生紹介 メネラウスの定理の覚え方はコレだ 証明 問題付き 高校生向け受験応援メディア 受験のミカタ




内分 Recherche Sur Twitter Twitter
Apr 04, チェバの定理、メネラウスの定理を知っていると秒殺できる問題もあり、使いこなせれば有利でしょう。 ただマイナス面もあります。 ・覚える時間がもったいない。 定理そのものを覚える必要と、どのような問題に定理を適応できるかを認識できるようにする必要がある。 ・本質の理解がおろそかになる。 応用が効かなくなる。 ・定理を使い間違える可能性がAug 04, 13とりあえずチェバの定理で bf:fc=2:3 を出してしまえば あとは 四角形dbceと直線afに着目して 定理を適用します~ もう1問やってみましょう~ 「五角形dbcgpと直線ae」,「 pfgと直線ae」 に着目して定理を適用することで(1)を解き,Feb 19, 21中点連結定理の応用 台形の中点連結定理;



数学i Aチェック リピート 第4章 2図形への応用 1 余弦定理 Pukiwiki




高1 数a チェバの定理 メネラウスの定理 授業ノート 高校生 数学のノート Clear
Feb 05, チェバの定理とその覚え方、チェバの定理の逆、例題をまとめました。 チェバの定理を使ってどうやって問題を解いたらいいのかわからない、点oが外部にあるときはどう式をたてたら良いのかわからないという方は参考にしてください。Oct 18, 18そう、それで、チェバの定理なの。洗いざらい問題をチェックしていて、出てきた。チェバの定理。はて?なんだっけ?私は全く記憶にない。 調べたら高校1年でやる、みたいなことが書か次の定理にちなんでこれらをチェバ図と呼ぶことにする。 チェバの定理 abcの内部に1点gがあり,線分ag,bg,cgの延長が対辺と交わる点をそれぞれd,e,fとするとき,次の公式が成り立つ。 チェバ図を見ればこの公式は明らかである。じっさい, となるからである。 この定理を示すには,次の3つの方法がある。



メネラウスの定理とは 証明や覚え方 問題の解き方 受験辞典




チェバの定理 メネラウスの定理を使う問題再び 2017年度前期日程の奈良女子大学環境学部入試問題 身勝手な主張
「チェバの定理の逆」に関する問題と数 学の考え方について いきなりですが、チェバの定理を使って解く有名問題と、その解答を掲載します。なぜ、 そのような解答にいたったか?ということは、解答の後に記載していくことにします。Nov 09, 1018年11月現在、中高一貫校の中学2年生を何人か指導しています。 幾何は、大体チェバの定理とメネラウスの定理の前後をやっているところです。 文部科学省検定教科書には載っていないと言っても、体系数学2(幾何)には、しっCoa boc =1 9 右の図のように,∠a=90°,ab=4 cm,bc=5 cm,ca=3 cm の abc がある。
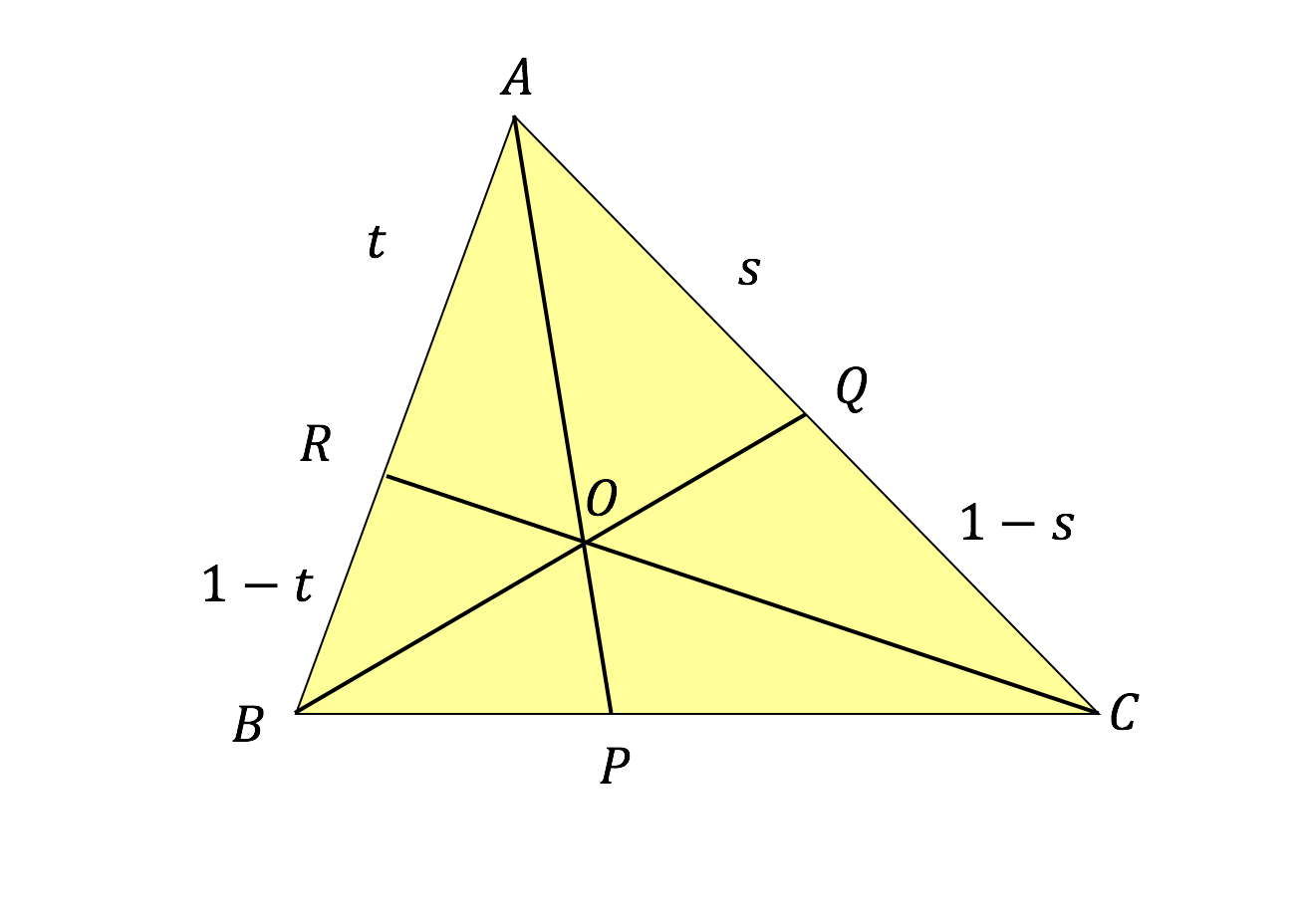



3分で分かる チェバの定理をわかりやすく 証明も徹底解説 合格サプリ



チェバの定理とは 証明や覚え方 メネラウスの定理との違い 受験辞典
点oは、 abcの内部にある点だね。 abcの内部にある点oと、各頂点を結んだときにできる線分比は、 チェバの定理 を使うことが多いんだけど、この問題で求めたいのはqo:ocなんだ。チェバの定理では、たどりつけない。そこで、見方を変えてみよう。




高1 数学a 3章 1節 三角形の性質 高校生 数学のノート Clear




高校数学a チェバの定理とメネラウスの定理の基本問題演習 受験の月
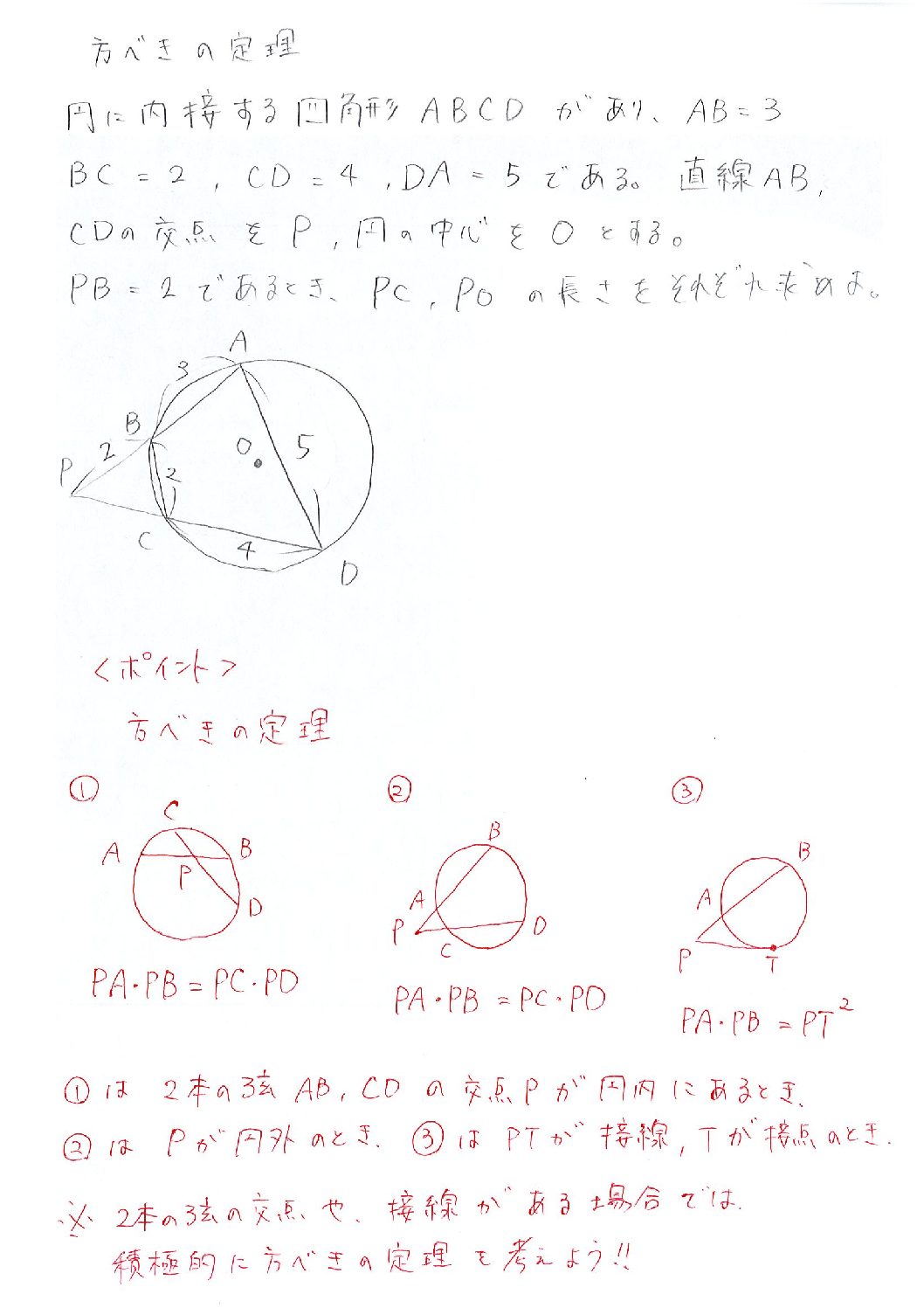



方べきの定理解説 塾を探す前に読むブログ




Dfracbddcdfracpbpc Dfracceea See How To Solve It At Qanda
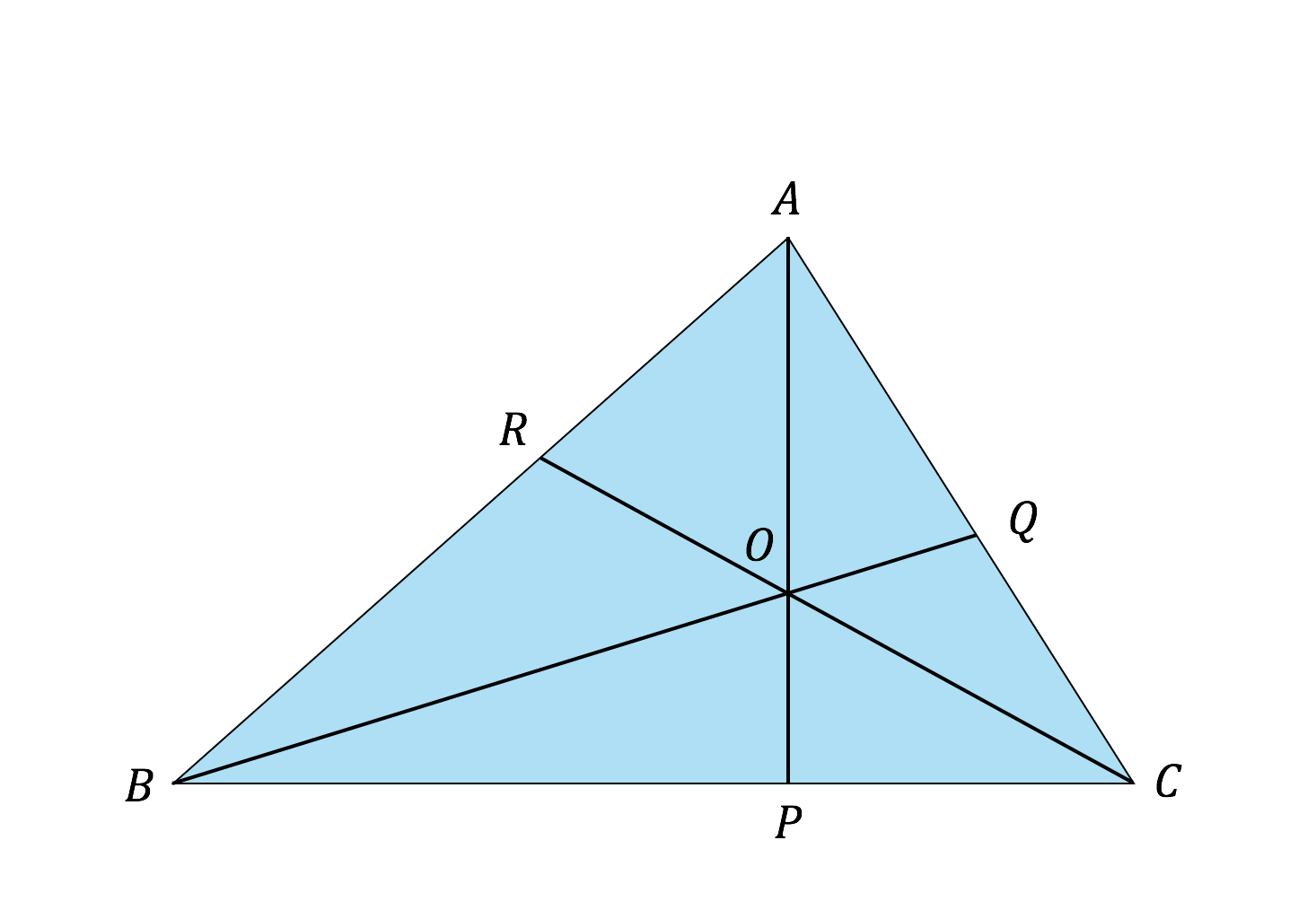



3分で分かる チェバの定理をわかりやすく 証明も徹底解説 合格サプリ




チェバの定理まとめ 証明 覚え方 逆 問題 理系ラボ




チェバの定理とメラネウスの定理を理解し問題を解ける Himokuri




平面ベクトル 2直線の交点 メネラウス型 オンライン無料塾 ターンナップ Youtube




メネラウスの定理 Menelaus S Theorem Japaneseclass Jp



新aクラス中学数学問題集3年 6訂版 市川 博規 著 文 昇龍堂出版 版元ドットコム



内分 Recherche Sur Twitter Twitter




Images Of チェバの定理 Japaneseclass Jp




チェバの定理 メネラウスの定理 超わかる 高校数学 A 授業 図形の性質 21 Youtube




高校数学a チェバの定理1 基本 練習編 映像授業のtry It トライイット




高校 数学a 図形18 チェバの定理2 10分 Youtube




三角形の面積比を解説 問題演習で平面図形をマスターしよう 応用編その3 中学受験ナビ




Mbaheblogjplu2q 70以上 メネラウスの定理 中学 メネラウスの定理 中学 問題




まだ公式まる覚えして消耗してるの チェバ メネラウスの定理 Youtube




チェバ メネラウスの定理の練習問題 9 Youtube



3分で分かる チェバの定理をわかりやすく 証明も徹底解説 合格サプリ




チェバの定理




チェバの定理とメラネウスの定理を理解し問題を解ける Himokuri




メネラウスの定理の逆について この問題で 答えの導きかたがbp Pc C Okwave




Ppt 数学のかた ち Powerpoint Presentation Free Download Id




チェバの定理は 三角形の内部にある点xと3頂点を結んだ直線が 3辺と交わる時に成り立 Clear



Ppt 数学のかた ち Powerpoint Presentation Free Download Id



チェバの定理とは 証明や覚え方 メネラウスの定理との違い 受験辞典




メネラウスの定理 Menelaus S Theorem Japaneseclass Jp




数学a 平面図形 メネラウス チェバの定理 まとめ集 自宅でできる受験対策ショップ ワカルー Wakaru




ベクトルは2時間で解けるようになる 外資系コンサルタントが主夫になったら




メネラウスの定理ってどういうときに使うのですか Okwave




寺子屋日誌



3分で分かる チェバの定理をわかりやすく 証明も徹底解説 合格サプリ




チェバの定理は 三角形の内部にある点xと3頂点を結んだ直線が 3辺と交わる時に成り立 Clear
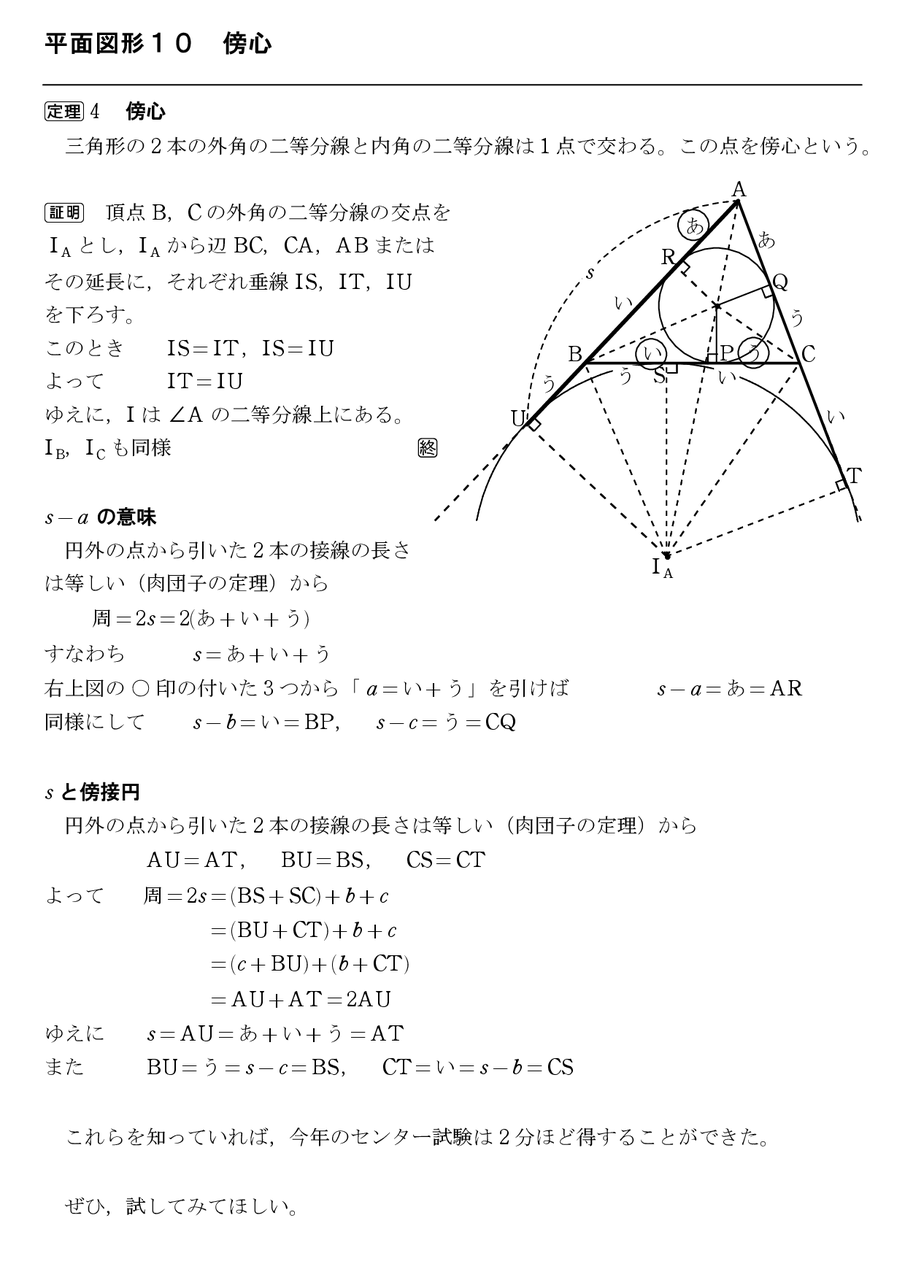



気ままに書き綴る 怜悧玲瓏 高校数学を天空から俯瞰する



数学ii Bチェック リピート 第3章 2方程式 不等式 最大 最小 8 図形への応用 Pukiwiki
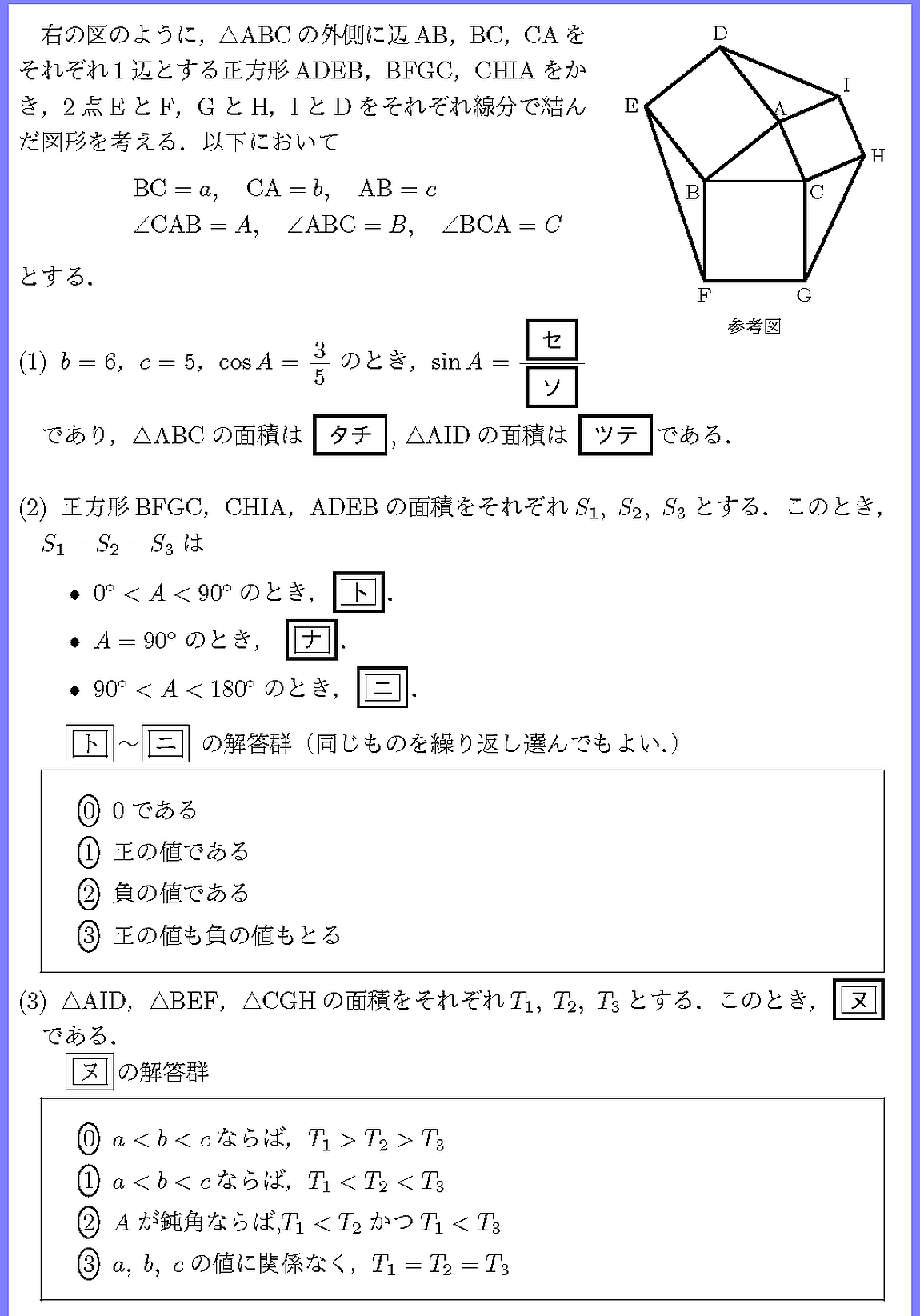



数学i Aチェック リピート 第4章 2図形への応用 4 外接円 内接円の半径 Pukiwiki




慶應生紹介 メネラウスの定理の覚え方はコレだ 証明 問題付き 高校生向け受験応援メディア 受験のミカタ



チェバの定理とは 証明や覚え方 メネラウスの定理との違い 受験辞典




Mbaheblogjplu2q 70以上 メネラウスの定理 中学 メネラウスの定理 中学 問題




高校入試file 003 数学 平面図形 三角形の面積比 ポイントは メネラウスの定理 Youtube



方べきの定理解説 塾を探す前に読むブログ



メネラウスの定理 Menelaus S Theorem Japaneseclass Jp



チェバの定理とは 証明や覚え方 メネラウスの定理との違い 受験辞典




平面図形11 メネラウスの定理の逆 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学a メネラウスの定理2 応用 例題編 映像授業のtry It トライイット




高校数学b 2直線の交点の位置ベクトル ベクトル分野ダントツno 1頻出問題 受験の月




数学i A




高校数学a チェバの定理2 応用 練習編 映像授業のtry It トライイット




高校数学a チェバの定理1 基本 練習編 映像授業のtry It トライイット




逆数学




チェバの定理まとめ 証明 覚え方 逆 問題 理系ラボ



受験 定期試験 数学解き方集 裏技 解法 メネラウス チェバの定理 中学 高校




新入試対応 数学i A基礎問題精講 五訂版 Amazon Com Books



新中学問題集シリーズ改訂特集 特集 教育開発出版株式会社



数学i Aチェック リピート 第4章 2図形への応用 10 空間図形の体積 Pukiwiki




Ppt 数学のかた ち Powerpoint Presentation Free Download Id




難問チェバ メネラウス 食塩濃度の問題を暗算で解く 悪魔の必殺技 天秤法 Studygeek スタディーギーク



チェバの定理とは 証明や覚え方 メネラウスの定理との違い 受験辞典




メルカリ Z会 数学 幾何編 参考書 1 000 中古や未使用のフリマ




2直線の交点 の裏技解法を知ろう 3パターンの解法



チェバの定理とは 証明や覚え方 メネラウスの定理との違い 受験辞典




高1 数学a 3章 1節 三角形の性質 高校生 数学のノート Clear




Paypayフリマ Z会数学アドバンスト 幾何2テキスト 問題集 解答編 3冊中高一貫教育数学研究会




授業での雑談ネタ 怜悧玲瓏 高校数学を天空から俯瞰する



3分で分かる チェバの定理をわかりやすく 証明も徹底解説 合格サプリ



3分で分かる チェバの定理をわかりやすく 証明も徹底解説 合格サプリ




2 164 Abc P Zbpc Zcpa Apb See How To Solve It At Qanda



0 件のコメント:
コメントを投稿